Жуто-зелени квадрати¶

Пошто знамо укупан број квадрата и ширину целог екрана дуж око којег су они распоређени, ширину једног квадрата можемо једноставно израчунати дељењем укупне ширине бројем квадрата. Квадрате цртамо у петљи. Ако вредност бројачке променљиве почиње од 0, тада се координата \(x\) левог горњег темена i-тог квадрата може добити множењем ширине квадрата бројем i (заиста, ако је ширина квадрата \(a\), тада квадрати редом почињу на координатама \(0, a, 2 a, \ldots, (n-1)\cdot a\). Координата \(y\) горњег левог темена сваког квадрата се добија одузимањем половине висине квадрата од средине екрана (коју израчунавамо дељењем висине екрана са два). На тај начин се вертикално средиште квадрата налази на средини екрана. На крају, боју квадрата можемо одредити у зависности од парности редног броја квадрата који се црта. Када је бројач у петљи i паран (када му је вредност 0, 2, 4, 6 или 8, што можемо израчунати поређењем остатка при дељењу i % 2 са нулом) тада квадрат бојимо у жуто, а када је непаран (када му је вредност 1, 3, 5, 7 или 9), тада квадрат бојимо у зелено.

Још један начин да се наизменично мењају боје је да се уведе логичка променљива којом се означава да ли цртамо жути квадрат. У почетку је постављамо на вредност тачно, у сваком кораку петље јој мењамо истинитосну вредност (тако што је негирамо оператором not), а у телу петље боју одређујемо на основу те вредности, гранањем.

Приметимо да смо наредбом гранања (наредби if-else) само поставили боју, а да смо сам квадрат цртали независно, након гранања. Наиме, да смо у наредби гранања цртали квадрат, непотребно бисмо понављали кôд и тиме начинили програм тежим за одржавање.

Могуће је још једно, суштински другачије решење овог задатка, које се не заснива на гранању, већ на листи у којој се памте боје које се циклично смењују. Редни број квадрата је одређен бројачком променљивом i, која редом узима вредности 0, 1, 2, 3, 4, … Са друге стране позиција боје у листи редом треба да узима вредности 0, 1, 0, 1, 0, … Можемо приметити да се та позиција може добити од вредности i тако што се израчуна остатак при дељењу са 2. Ово се лако може уопштити и на више од две боје. Када би се наизменично смењивале 3 боје, тада би позиције требало да узимају вредности 0, 1, 2, 0, 1, 2, … и добијале би се израчунавањем остатка при дељењу са 3. У општем случају, потребно је израчунати остатак при дељењу дужином листе. На основу ове дискусије покушај да допуниш наредни код.

Патент затварач¶

Покушај и овај задатак да решиш коришћењем листе, без гранања (овај пут ћеш у листу сместити две позиције почетка линије).

Плесни подијум¶

Претпоставићемо да на располагању имамо функцију која на насумичан начин одабире боју (њу је веома једноставно испрограмирати коришћењем функције random.randint). Угнежђеним петљама ћемо набрајати све парове \((0, 0)\), \((0, 1)\), …, \((0, n-1)\), \((1, 0)\), …, \((1, n-1)\), …, \((n-1, 0)\), …, \((0, n-1)\). Задатак се онда своди на то да одредимо горње лево теме квадрата који се налази у врсти са редним бројем \(i\) и колони са редним бројем \(j\). Пошто се лево од тог квадрата налази тачно \(j\) квадрата, док се изнад њега налази тачно \(i\) квадрата, координате његовог горњег левог темена су \((j*a, i*a)\). На основу овога лако можеш допунити наредни код.

Сивкасти насумични кружићи¶

Овај задатак је сличан претходном, једино што су нам уместо горњих левих темена сваког поља потребне координате центра сваког поља. За свако поље насумично генеришемо полупречник (цео број из интервала \([2, d]\)), нијансу сиве боје (цео број из интервала \([0, 255]\)) и на основу боје, координата центра и полупречника вршимо цртање круга. Подсетимо се, за насумични одабир целог броја из интервала \([a, b]\) користимо функцију random.randint(a, b).

Покушај да самостално урадиш овај задатак. Ако не успеваш, онда искористи понуђену помоћ, па допуни започети програм.

Зграда¶

Зграда коју треба да нацртамо је приказана на наредној слици.

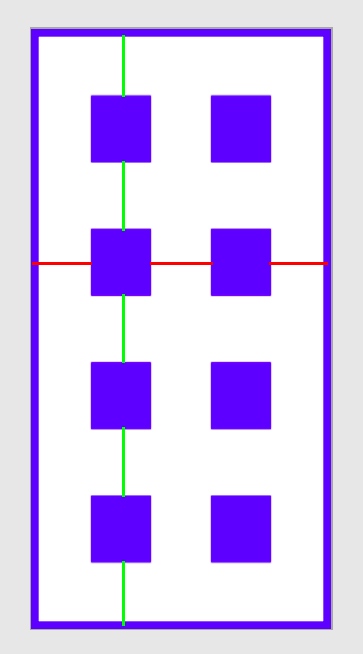
Зеленом бојом су означени међуспратови, укључујући и простор испод првог спрата и изнад последњег спрата, док су црвеном бојом означене међувертикале, укључујући и простор лево од прве и десно од последње вертикале. Видимо да је број међуспратова за један већи од броја спратова, док је број међувертикала за један већи од броја вертикала. Претпоставићемо да је висина сваког прозора иста као висина сваког међуспрата и да је ширина сваког прозора једнака ширини сваке међувертикале. Одавде можемо израчунати висину прозора зграде (тако што укупну висину поделимо са збиром броја спратова и међуспратова) и ширину прозора зграде (тако што укупну ширину поделимо са збиром вертикала и међувертикала). Прозоре можемо цртати од горе на доле (иако се спратови увек броје од доле на горе). Координате горњег левог темена прозора у врсти \(i\) и колони \(j\) можемо добити тако што на ширину међувертикале додамо \(j\) пута збир ширине прозора и ширине међувертикале (што је у нашем случају једнако двострукој ширини прозора) тј. тако што на ширину међуспрата додамо \(i\) пута збир висине спрата и висине међуспрата (што је у нашем случају једнако двострукој ширини међуспрата).

Покушај да на основу претходне дискусије самостално урадиш овај задатак. Ако не успеваш, онда искористи понуђену помоћ, па допуни започети програм.

Уместо петљи у којима се редом наводе редни бројеви, могли смо употребити и петље са кораком.

Покушај сада да прилагодиш претходни програм тако да висина међуспрата буде само пола висине спрата.

Шаховска табла¶

Овај задатак је веома сличан оном у ком смо цртали плесни подијум. Главна разлика је у томе што се боја не одређује насумично, већ се наизменично смењују црна и бела поља. Можемо позадину целе табле обојити у бело, а затим исцртати само црна поља. Главни изазов у овом задатку је како на основу редног броја врсте i и редног броја колоне j одредити да ли се на том месту налази црни или бели квадрат. Покушај да одредиш ово правило, а ако не успеш, онда погледај решење.

Домаћи задатак - паркет¶

Овај задатак представља комбинацију два задатка који смо раније радили: шпартања екрана вертикалним линијама и шаховске табле. Покушај да самостално урадиш овај задатак. Ако не успеваш, онда искористи понуђену помоћ, па допуни започети програм.